The worst-case analysis gives a theoretical upper bound on the algorithmic performance. It’s important but, it has its limitations. So, there are other kinds of analyses to fill those gaps.

Outline

Average Case Analysis

• ‘average cost’ over all the inputs.
• It’s possible for some inputs to perform more poorly than the rest but, assuming that every input is equally likely to occur, the impact of those inputs might be low in real-time.
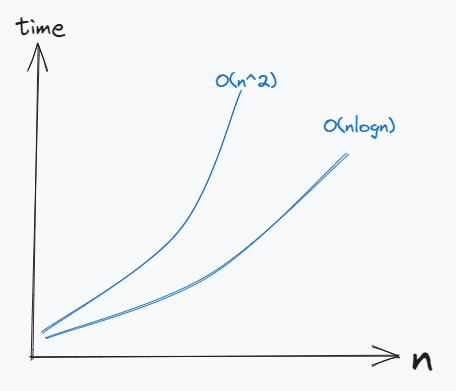
• For example, in some implementation of quicksort it’s possible that for a (nearly) sorted array, the time complexity is O(n^2). But, for a sufficiently large n, those inputs would be very rare.
• upon averaging the cost across all the inputs, the average cost will still be O(nlogn).
• NOTE1: the ‘worst case’ metes out the punishment of the worst input to all inputs. Thus, for the above case, the worst case time complexity is O(n^2).
• NOTE2: the ‘average case’ distributes the punishment of worst inputs over all the whole input space.

Probabilistic Analysis

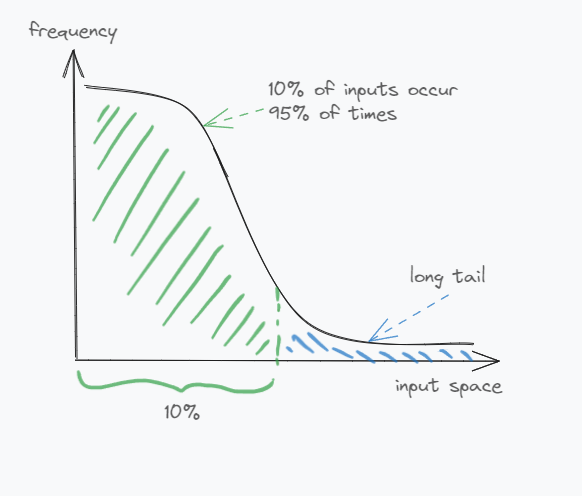
• this is similar to average case except that probabilistic analysis distributes the cost of the algorithm using a weighted average of the probability of an input to occur as opposed to average case which distributes the bad performance of a few inputs evenly.
• this plugs the hole of long tail problem in the input space where ‘some’ inputs may occur ‘most’ of the time.
• for example, we might have a problem statement where we almost always get a sorted array as an input and very rarely an unsorted one. With the quicksort implementation from the average case analysis, the real performance will (almost) always be O(n^2) i.e. close to worst-case than the average case. maybe, to remediate that we might want to introduce some check for sorted-ness.
• maybe our inputs will always be either 0 or 1 in which case might want to question the use of quicksort itself.
• NOTE1: the probabilistic analysis takes the input space distribution into account unlike other analysis methods.
• NOTE2: the ‘worst case’ of quicksort is still O(n^2) and the ‘average case’ is still O(nlogn).

Amortized Analysis

• ‘average cost’ over a sequence of operations.
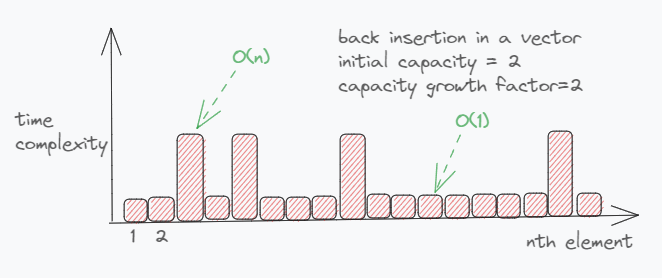
• for example, a vector insertion in the back is O(1) when size < capacity but, O(n) when size == capacity because of reallocation and move of elements from old memory locations to the new.
• Now, with a very poor implementation of capacity expansion which increases the capacity by 1, once the initial capacity is exhausted, you’ll be in a perpetual state of inserting elements into a fully utilised vector making every operation as O(n) with the amortized time complexity of O(n).
• But, if the capacity increases by, say, a factor of 2, the number of reallocations for the same number of elements decreases exponentially with every increase in capacity effectively making back insertion as O(1) for almost all cases with a very few O(n) operations making the amortized time complexity as O(1).
• NOTE1: the ‘worst case’ is still O(n).
• NOTE2: unlike the average case, amortized analysis isn’t looking at the input rather, it considers the sequence of operations.

Real-Time Performance

• while theoretical analysis of algorithms helps to reason about and narrow down the implementation candidates, the real-time performance is ultimately what matters. with a better on-paper time-complexity, it’s possible for an algorithm to perform worse than its counterparts.
• for example, the sorting implementation in the standard lib of many languages opt for a hybrid approach where they use insertion sort for small vectors which has an average and worst case of O(n^2) or similarly for small vectors, a linear search may be better than binary search. Both because of locality of reference of the elements leading to more cache-hits.